Machine learning contains a treasure trove of algorithms attempting to comprehend data, but none of them match the accuracy of Support Vector Machines (SVMs). SVMs were first made for classification and have now been turned into an all-purpose utility for regression, outlier detection, and even text processing. They excel at processing high-dimensional data and hence remain the preferred algorithm for problems on which other techniques fail.

But what makes SVMs perform so well? The key is their capacity to generate boundaries between multiple groups in a dataset with optimal separation, achieving the most accurate classification possible.

Understanding the Core Concept of SVM

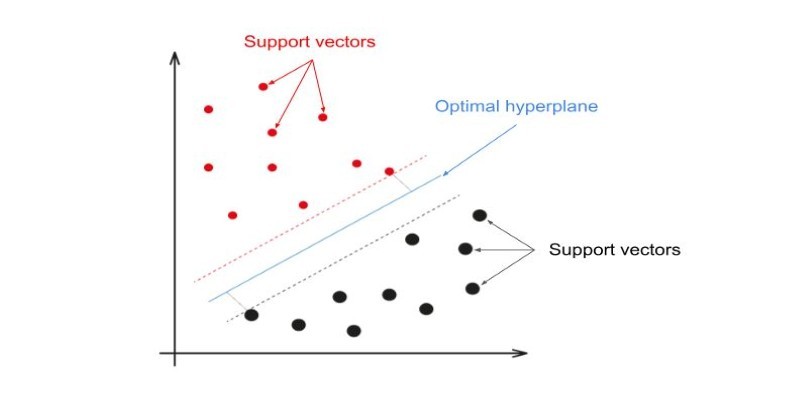
At its core, a Support Vector Machine tries to determine the optimal dividing line—or decision boundary—between multiple categories in a dataset. You have two categories of objects tossed about on a graph. SVM goes about trying to draw the most ideal line, referred to as a hyperplane, between them. Its purpose is to position this boundary such that the distance between each category's nearest points is at maximum. These nearest points are referred to as "support vectors," and they are important in determining the decision boundary.

This method is called maximizing the margin. The higher the margin, the more well the model generalizes to new data, lowering the risk of misclassification. When data is cleanly separated, the job is easy. Real-world datasets are not that nice, though. They tend to have overlapping points, outliers, or non-linear distributions, so classification becomes problematic. That's where SVM's power to map data to higher dimensions comes into play.

How SVM Handles Complex Data?

Not all problems can be solved by a straightforward straight-line boundary. Some datasets need more evolved techniques to distinguish various groups. SVM resolves this issue using the kernel trick. This technique enables SVM to transform data into higher dimensions, where the data is easier to separate using a boundary.

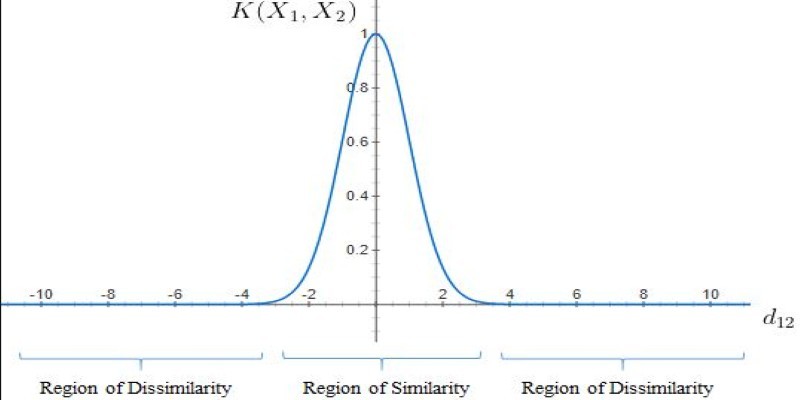
For instance, if a dataset looks inseparable in two dimensions, SVM can project it into a three-dimensional space where a clear boundary emerges. Common kernel functions include:

• Linear Kernel: Best for cases where the data can be separated with a straight line.
• Polynomial Kernel: Useful when the relationship between data points is more complex.
• Radial Basis Function (RBF) Kernel: Effective for datasets with intricate patterns, creating flexible decision boundaries.
• Sigmoid Kernel: Sometimes used for neural network-inspired transformations.

By choosing the right kernel, SVM can adapt to different types of data structures, making it an incredibly flexible machine-learning tool.

Applications of SVM in the Real World

The versatility of SVM extends far beyond theoretical applications. Many industries rely on it to classify and predict patterns in large datasets. One of the most common areas is image classification, where SVMs help distinguish between objects in a photo, recognize handwriting, and even detect medical anomalies in MRI scans. Due to their ability to handle high-dimensional data, SVMs are particularly effective in face detection and optical character recognition (OCR) tasks.

Another major use case is text and speech recognition. Email spam filters, for example, often use SVMs to differentiate between legitimate messages and junk mail. Similarly, voice recognition systems employ SVMs to identify spoken words and phrases with remarkable accuracy.

In finance, SVMs detect fraudulent transactions by identifying unusual patterns in spending behavior. Since fraud detection involves recognizing subtle deviations from normal activities, SVMs' ability to handle high-dimensional data proves invaluable.

SVMs also benefit the healthcare industry. In disease prediction, they help analyze medical records to detect early signs of conditions like cancer, heart disease, or diabetes. By training an SVM on large datasets containing past patient data, doctors can make informed predictions about a patient's health risks.

Strengths and Limitations of SVM

SVMs have several advantages that make them a preferred choice for many machine-learning tasks. Their biggest strength is their robustness against high-dimensional data. Unlike other algorithms that struggle with numerous features, SVM performs exceptionally well even when the dataset contains thousands of variables.

Another key advantage is generalization ability. Since SVM maximizes the margin between classes, it often results in models that perform well on unseen data, reducing the chances of overfitting. Additionally, SVMs are effective even when the dataset is relatively small, making them an excellent choice when limited labeled data is available.

However, despite these strengths, SVM is not without limitations. One major challenge is computational complexity. Training an SVM, especially with non-linear kernels on large datasets, can be time-consuming and require significant computational power. This makes it less practical for big data applications compared to algorithms like deep learning.

Another drawback is sensitivity to noisy data. SVM relies heavily on support vectors, meaning that outliers can significantly affect the decision boundary. If the dataset contains too much noise, SVM might struggle to generalize properly.

Finally, choosing the right kernel function can be difficult. While SVM provides several kernel options, selecting the best one for a given dataset requires trial and error. A poor choice of kernel can lead to suboptimal results, requiring domain expertise to fine-tune the model effectively.

Conclusion

Support Vector Machines remain a cornerstone of machine learning due to their remarkable accuracy, versatility, and ability to handle complex datasets. Whether it's classifying images, recognizing text, detecting fraud, or predicting diseases, SVMs have proven their reliability across a range of applications. Their strength lies in their ability to create optimal decision boundaries, particularly in high-dimensional spaces. Despite their computational challenges, SVMs continue to be a preferred tool for many real-world tasks, especially when data is limited or high precision is required. As machine learning evolves, SVMs remain highly relevant, serving as a powerful alternative to deep learning methods for many classification and regression problems.